The Diffie-Hellman key agreement algorithm

Diffie-Hellman is a key-agreement algorithm. It allows two peers to agree on the same symmetric key, the shared secret, without exchanging confidential data.

The Diffie-Hellman key agreement algorithm is a method that allows two devices to communicate over a network by establishing a shared secret without exchanging any secret data. Knowing the used key-agreement algorithm, the two devices only need to exchange their public key. Then, using the other peer's public key and its own private key, each device performs the algorithm specific key generation operation to obtain the shared secret. The shared secret is a ready-to-use symmetric key for further signed or encrypted exchanges between the two peers.

Genero Web Services provides several shared secret type for signature, encryption, or key encryption purposes. Using the Diffie-Hellman key agreement algorithm, one of the following types of shared secrets can be computed:

Symmetric AES128 encryption key
Symmetric AES192 encryption key
Symmetric AES256 encryption key
Symmetric TripleDES encryption key
Symmetric key wrap AES128 key encryption key
Symmetric key wrap AES192 key encryption key
Symmetric key wrap AES256 key encryption key
Symmetric key wrap TripleDES key encryption key
Symmetric HMAC-SHA1 signature key

In the Diffie-Hellman key agreement algorithm, two shared constants (called parameters) are used in addition to the private and public key. These two parameters are:

The modulus (called P): A very big prime number chosen at random.
The generator (called g): A prime number between two and five. Genero Web Services only uses two (2) for the generator.

If the private key (Priv) is a big number (not necessarily prime) chosen randomly, the public key (Pub) is calculated using P, g, and Priv as follows:

Pub = g^Priv mod P

Both devices need to use the same parameters for P and g. There are two ways to ensure this happens: Either P and g are chosen by a third party (such as a security authority) or one of the devices chooses them and sends them to the other peer with its public key.

Genero Web Services allows the Web service to generate the parameters itself, to load them from a string or from a PEM or DER file. The public key and the parameters can also be exchanged using an XML file.

This diagram shows the Diffie-Hellman algorithm steps between two devices, A and B, that need to communicate. Device A is in charge of generating the parameters. The shared secret is labeled K.

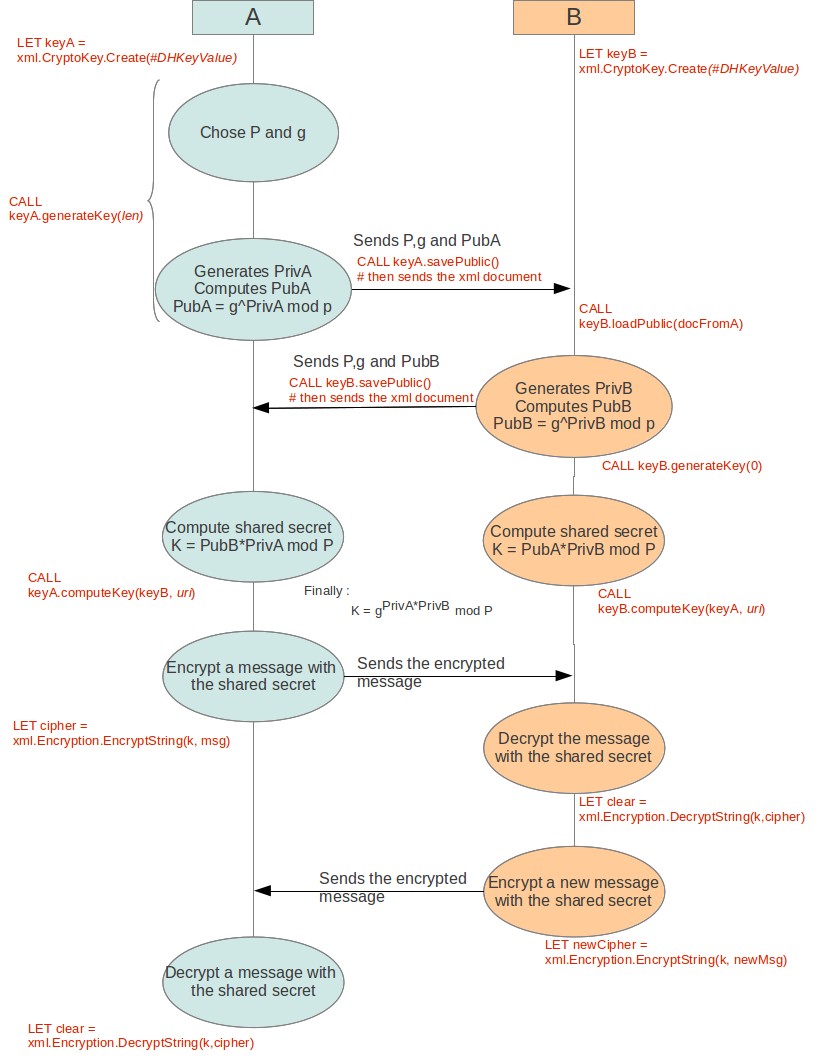
Diagram showing how Diffie-Hellman works between two devices labeled A and B. On A, we start with LET keyA=xml.CryptoKey.Create(#DHKeyValue). On B, we have LET keyB=xml.CryptoKey.Create(#DHKeyValue). A then chooses P and g. A then executes CALL keyA.generateKey(len). A Generates Private key for A (PrivA), then computes Public key for A (PubA) using the formula PubA=g^PrivA mod P. A sends P, g, and PubA to B. It issues CALL keyA.savePublic(), then sends the XML document. On B, we have CALL keyB.loadPublic(docFromA). B then generates its PrivB, computes its PubB, then Sends P, g, and PubB back to A by CALL keyB.savePublic() and sending the XML document. B then issues CALL keyB.generateKey(0). Both A and B now compute the shared secret: for A, shared secret K = PubB * PrivA mod P; for B, shared secret K = PubA * PrivB mod P. On A: CALL keyA.computeKey(keyB, url). On B: CALL keyB.computeKey(keyA, url). Now A can encrypt a message with the shared secret: LET cipher=xml.Encryption.EncryptString(k, msg). It sends the encrypted message to B. B decrypts the message: LET clear=xml.Encryption.DecryptString(k,cipher). B can then encrypt a new message: Let newCipher=xml.encryptionl.EncryptString(k,newMsg) and send back to A, who can now decrypt: LET clear=xml.Encryption.DecryptString(k, cipher).

Figure 1. The Diffie-Hellman algorithm

For complete details about the mathematical basics underlying the Diffie-Hellman algorithm, see [RFC2631].

It is nearly impossible to get the private key from the public key, even knowing the values of parameters P and g. Therefore, a middle man will not be able to obtain the shared secret K. While devices A and B exchange their public key, and maybe the parameters as well, these values pass through different intermediate points. It is critical that A receives the correct public key from B, and that B receives the correct public key from A, in order to establish a common shared secret. A middle man could corrupt or replace one public key with his own. If that happens, A and B would be able to communicate because they won't compute the same shared secret. No secret data will be exchanged and readable to the middle man. To avoid this situation, one can use Digital Certificate that helps to deliver the public key and the parameters in an authenticated method.

Once the shared secret is established, the Diffie-Hellman public key, private key and parameters are no longer useful. The Diffie-Hellman key agreement algorithm is achieved.

With the library provided as part of Genero Web Services, the shared secret has been computed to fit given specifications such as HMAC, 3DES, AES128, AES192, AES256, KW-3DES, KW-AES128, KW-AES192, or KW-AES256. The shared secret is actually a symmetric key ready to be used in a signature (HMAC) or cipher algorithm. It allows devices A and B to finally communicate via an authenticated (HMAC) or encrypted method.